Un día Gauss estaba sentado en una no tan interesante lección de matemáticas haciendo origami con una $a \times b$ rectangular hoja de papel $(a>b)$. Por lo general el primer paso para hacer origami es hacer una pieza cuadrada de papel de la hoja rectangular doblando la hoja a lo largo de la bicectríz del angulo rectángulo, y cortar la parte que se excede.

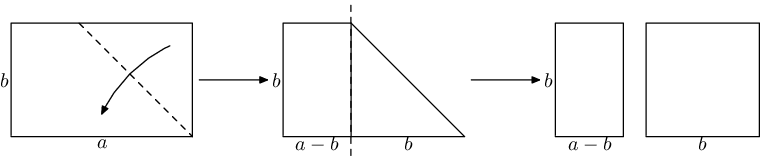
Después de hacer un barco de papel de la pieza cuadrada, Gauss miró la restante $(a-b) \times b$  tira de papel. Él tuvo la idea de usar esta tira de papel de la misma manera para hacer otro origami, y luego usar el resto (si existe) y así sucecivamente. En el momento en el que se queda con un pedazo cuadrado de papel, se hará el último barco y  se detendra.

¿Puedes determinar cuántos barcos de papel Gauss hará durante la lección?

La primera línea contendra un número entero $T \; (1 \leq T \leq 100)$, el número de casos de prueba. Seguidamente se le dara $T$ líneas, cada una conteniendo dos enteros $a, \; b \; (1 \leq b < a \leq 10^{12})$, el tamaño de la pieza original de papel.

Imprimir $T$ lineas, cada una conteniendo el número de barcos que Gauss puede hacer.

 Simular el proceso hasta que la division a / b sea exacta