Copiado al portapapeles
Descripción
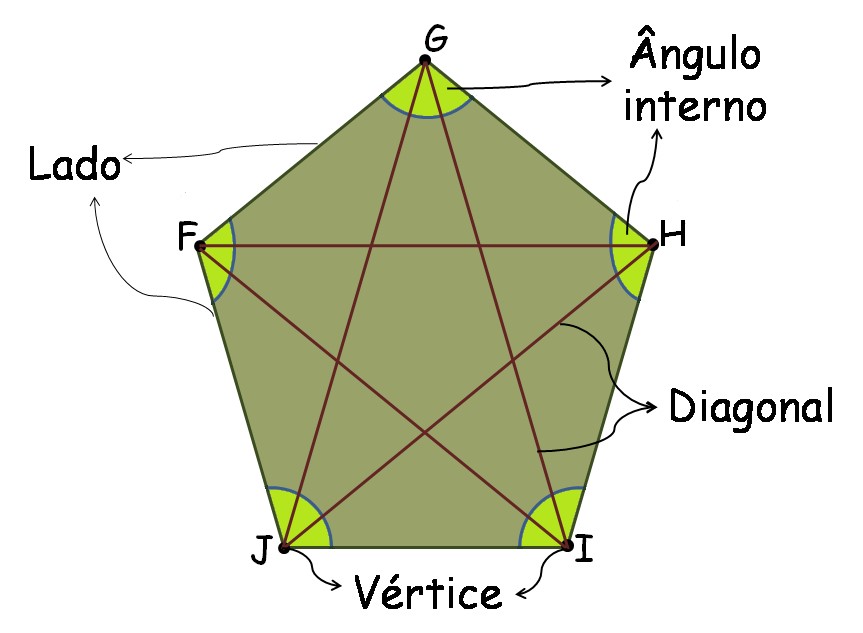
En geometría, un polígono es una figura geométrica plana compuesta por una secuencia finita de segmentos rectos consecutivos que encierran una región en el plano.
En este caso trabajaremos con polígonos regulares cuyos lados y ángulos interiores son iguales entre sí.
Donde:
$C_l =$ cantidad de lados de un polígono regular.
$C_d =$ cantidad de diagonales de un polígono regular.
El problema pide hallar el número de vértices de un polígono regular dado $N = C_l + C_d $
En este caso tendremos $N = 10$ porque $C_l = 5$ y $C_d = 5$ por lo tanto la cantidad de vértices es igual a 5
Entrada
La entrada consiste en un numero entero N $(3\leq N \leq 5*10^{13})$ donde $N = C_l + C_d$
Salida
Imprimir la cantidad de vértices del polígono regular donde $N = C_l+C_d$ (Se garantiza que existe una respuesta).
Ejemplo Entrada
10
Ejemplo Salida
5
Ayuda
2da div. 2017 UMSA