Debido a la pandemia que atraviesa el mundo, las autoridades de la ciudad obligaron a los ciudadanos a mantener una distancia social. El alcalde de la ciudad quiere iluminar el parque PATITO para que la gente pueda verse incluso de noche para mantener la distancia social.

El parque es una cudricula rectangular con $n$ filas y $m$ columnas, donde las celdas de la tabla son cuadrados y los límites entre las celdas son calles. Las fronteras exteriores también son calles. Cada calle tiene una longitud de $1$. Por ejemplo, el parque con $n = m = 2$ tiene $12$ calles.

Se le asignó desarrollar un plan para iluminar el parque. Puedes poner linternas en medio de las calles. La lámpara ilumina dos cuadrados cerca de ella (o solo un cuadrado si se encuentra en el borde del parque).  

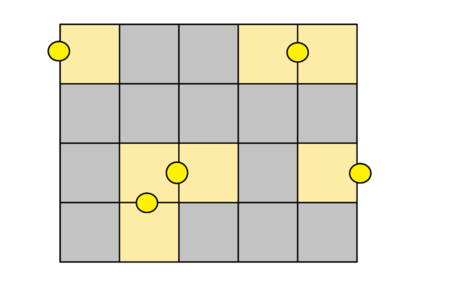
Los tamaños del parque son: $n = 4$, $m = 5$. Los cuadrados iluminados están marcados en amarillo. Tenga en cuenta que todas las calles tienen una longitud de $1$. Las linternas se colocan en el medio de las calles. En la imagen no todos los cuadrados están iluminados.
Semyon quiere gastar la menor cantidad posible de dinero en iluminación, pero también quiere que la gente de todo el parque mantenga una distancia social. Entonces te pide que encuentres el número mínimo de linternas que se requieren para iluminar todos los cuadrados.

La primera línea contiene un solo entero $t$ ($1 \leq t \leq 10^{4}$): el número de casos de prueba en la entrada. Luego siguen $t$ casos de prueba.

Cada caso de prueba es una línea que contiene dos números enteros $n$, $m$ ($1 \leq n, m \leq 10^{4}$) - tamaño del parque. 

Imprima $t$ respuestas a los casos de prueba. Cada respuesta debe ser un número entero: el número mínimo de linternas que se requieren para iluminar todos los cuadrados.

Posible disposición óptima de las linternas para el segundo caso de prueba del ejemplo de datos de entrada:

Posible disposición óptima de las linternas para el tercer caso de prueba del ejemplo de datos de entrada: