Después de ganar oro y plata en IOI 2014, Akshat y Malvika quieren divertirse. Ahora están jugando un juego en una cuadrícula hecha de $n$ palos horizontales y $m$ verticales.

Un punto de intersección es cualquier punto de la cuadrícula que está formado por la intersección de un palo horizontal y un palo vertical.

En la cuadrícula que se muestra a continuación, $n = 3$ y $m = 3$. Hay $n + m = 6$ palos en total (los palos horizontales se muestran en rojo y los verticales en verde). Hay $n · m = 9$ puntos de intersección, numerados del $1$ al $9$.

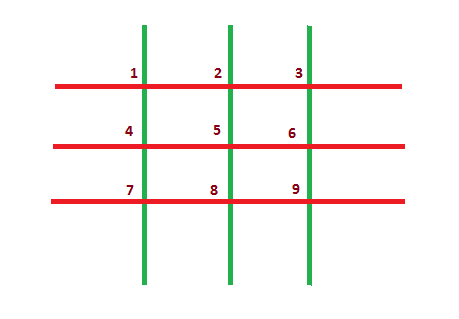
Las reglas del juego son muy sencillas. Los jugadores se mueven por turnos. Akshat ganó el oro, por lo que da el primer paso. Durante su movimiento, un jugador debe elegir cualquier punto de intersección restante y eliminar de la cuadrícula todos los palos que pasen por este punto. Un jugador perderá el juego si no puede hacer un movimiento (es decir, no quedan puntos de intersección en la cuadrícula en su movimiento).

Suponga que ambos jugadores juegan de manera óptima. ¿Quién ganará el juego?

La primera línea de la entrada contiene un número entero $t$ ($1 \leq t \leq 1000$): el número de casos de prueba. Cada caso de preba contiene dos números enteros separados por espacios, $n$ y $m$ ($1 \leq n, m \leq 100$).

Para cada caso de prueba, imprime una sola línea que contenga "$Akshat$" o "$Malvika$" (sin las comillas), dependiendo del ganador del juego.

Explicación del primer caso:

La cuadrícula tiene cuatro puntos de intersección, numerados del $1$ al $4$.

Si Akshat elige el punto de intersección $1$, quitará dos palos ($1-2$ y $1-3$). La cuadrícula resultante se verá así.

Ahora solo queda un punto de intersección restante (es decir, $4$). Malvika debe elegirlo y quitar los dos palos restantes. Después de su movimiento, la cuadrícula estará vacía.

En la cuadrícula vacía, Akshat no puede hacer ningún movimiento, por lo que perderá.

Dado que los $4$ puntos de intersección de la cuadrícula son equivalentes, Akshat perderá sin importar cuál elija.