Considere un grafo G formado por un numero grande de arcos interconectados. Se dice que G es conectado si se puede encontrar un camino en 0 o mas pasos entre cualquier par de nodos de G.

Por ejemplo el gráfico que se muestra no esta conectado porque no hay un camino entre A y C.



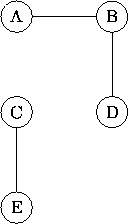
Este contiene sin embargo un numero de subgrafos que están conectados, uno por cada uno de los siguientes conjuntos de nodos: {A}, {B}, {C}, {D}, {E}, {A,B}, {B,D}, {C,E}, {A,B,D}.

Un grafo conectado es máximo si no existen ndos y arcos en grafo originar que puedan agregarse al subgrafo y que siga conectado. En el grafo del ejemplo hay dos subgrafos máximos, uno asociado a los nodos {A, B, D} y el otro asociado a los nodos {C, E}.

Escriba un programa para determinar el numero subgrafos máximos que existen en un grafo dado.

La entrada comienza con un numero entero positivo en una linea indicando el numero de casos de prueba que siguen. Esta linea esta seguida de una linea en blanco. También existe una linea en blanco entre dos entradas consecutivas.

La primera de cada caso de prueba contiene un solo caracter en mayúsculas. Este caracter representa el nombre de nodo más grande. Cada linea sucesiva contiene un par de letras mayúsculas que denotan un aro del grafo. El ejemplo corresponde al grafo mostrado.

La entrada se termina con una linea en blanco.

Para cada caso de prueba escriba el máximo numero de grafos conectados. La salida de dos casos consecutivos debe separarse por una linea en blanco.