Un USB Dead Drop es un dispositivo USB instalado en un espacio público. Por ejemplo una memoria flash USB podría estar montada en un muro y fijada con concreto. El nombre viene de la técnica ``Dead Drop'' de espionaje de comunicaciones. Estos dispositivos fueron colocados por todo el mundo por los hacktivistas.

Los hackers Alan y Botas están a punto de ejecutar una operación muy importante en su universidad ``Instituto Científico Patito Corcho'' (ICPC) que se encuentra en la ciudad de Río Fugitivo. El edificio principal del ICPC (también conocido como Monoblock) tiene jardines a sus costados, en los cuales los árboles están colocados de una forma muy característica gracias a la gente de la Carrera de Ciencias de la Computación. En cada uno de estos árboles se encuentran Dead Drops y Alan y Botas deben recuperar toda la información de estos para que su operación secreta tenga éxito.

La forma en que los árboles están plantados en el jardin es la de un árbol binario perfecto (ver la Figura 2), en las cuales los árboles son los nodos y los caminos del jardín los arcos.

Se te da el entero $N$ que indica la altura de el árbol (La altura de un árbol binario perfecto es el número de arcos en el camino entre el nodo raiz y alguno de los nodos hoja). Por lo tanto hay $2^{N+1}-1$ árboles con Dead Drops y $2^{N+1}-2$ caminos en el jardín en total.

La imagen de abajo muestra cómo luce el jardín cuando $N = 2$.

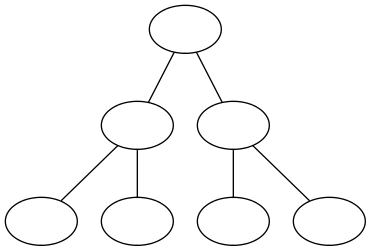
Alan y Botas son unos buenos nerds, y por esta razón quieren minimizar la cantidad de personas que irán a recoger la información de los Dead Drops. Cada persona que recogerá la información de un Dead Drop, visitará un árbol de inicio y un árbol fin sin visitar un árbol dos veces. (Note que la ruta de cada persona está unicamente determinada por el árbol de inicio y final). Es probable que el árbol de inicio sea el mismo que el árbol final, en este caso la persona solo visitará un árbol.

Ayuda a nuestros hackers a calcular la mínima cantidad de personas que necesitan si cada árbol solo puede ser visitado por una persona.

Primero debes leer un entero t ($1 \leq t \leq 10^4$) que indica la cantidad de casos de entrada. Luego por cada caso de entrada debes leer un N ($0 \leq N \leq 1000 $).

Por cada entrada imprimir la cantidad de personas que se necesitarán para recorrer por todos los árboles del jardín sin que dos personas pasen por el mismo árbol modulo 1000000007.