El 18 de junio de 1815, se observa a ambos lados del campo de batalla en Waterloo, los ejercitos napoleonicos y el ejercito de la septima coalicion que buscaba derrotar finalmente a Napoleon, pero su comandante el duque de Wellington Arthur Wellesley (la pesadilla de Napoleon) sabe que sus fuerzas son inferiores, es por eso que debe resistir el ataque de Napoleon hasta la llegada de refuerzos comandados por el mariscal prusiano Blucher. Wellesley ha decidido usar la tecnica que aprendio en el Instituto de Cartografia Para Coroneles(ICPC); al cual Napoleon nunca asistio pues ascendio directamente a general despues del sitio de Toulon, y no conoce la maniobra.

Wellesley se ha dado cuenta que el campo de batalla es en realidad un poligono regular de n lados, asi que ha decidido dividir el poligono en triangulos adicionando segmentos entre los vertices y sin que ningun par de segmentos se cruce, y coloca a cada una de las secciones de su ejercito defendiendo cada triangulo, y asi dividir al ejercito de Napoleon.

La clave del exito de la triangulacion, reside en que si algun triangulo del campo de batalla esta a punto de ser tomado por el ejercito napoleonico, otra fraccion del ejercito debe ir a recuperarlo, por tanto es necesario escoger una triangulacion en la cual la distancia que debe recorrer una seccion del ejercito para ayudar a otra sea minima.

Por ejemplo en la siguiente triangulacion la distancia mas larga se da entre los triangulos a y d, por tanto a la seccion 'A' del ejercito le toma 3 unidades de tiempo llegar en ayuda de la seccion 'D'

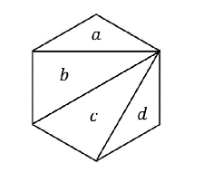
Pero es posible contruir una mejor triangulacion, en la que la maxima distancia que debe recorrer un ejercito para ayudar a otro sea menor que el anterior.

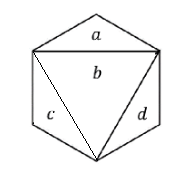
Cuya maxima distancia es 2 (a-c, c-d, a-d). Como no se puede encontrar otra triangulacion que mejore la maxima distancia, decimos que esta triangulacion es optima.

Varias lineas con enteros n ($3 \leq n \leq 10^5$) indicando el numero de lados del poligono.

Un entero unico con la distancia maxima que debe recorrer una seccion del ejercito para ayudar a otro, si se elige la triangulacion optima.